In 1990, Werner Fischer and Elke Koch classified embedded triply periodic minimal surfaces that can be obtained by extending Plateau solutions for Euclidean polygons. Below is one of their many fascinating examples.


Above on the left you see a minimal 8-gon, extended to a twisted minimal annulus on the right. The horizontal lines make a 60 degree angle, and if the height of the shorter vertical segments is one half of the gap size between two of these segments, further rotations will deliver an embedded surface.
It is hard to believe that something like this is possible, isn’t it?


Hermann Karcher describes a variation of this construction that creates 6-ended singly periodic minimal surfaces. He also mentions that these surfaces can be twisted, i.e. deformed into screw-motion invariant minimal surfaces with helicoidal ends.


Above you can see what happens when the surface is twisted clockwise. On the right, we approach a parking garage structure with five helicoidal columns, four of them with positive spin and axes at the corners of a square, and one with negative spin at the center of the square. Not getting lost in a parking garage like this would be very difficult…
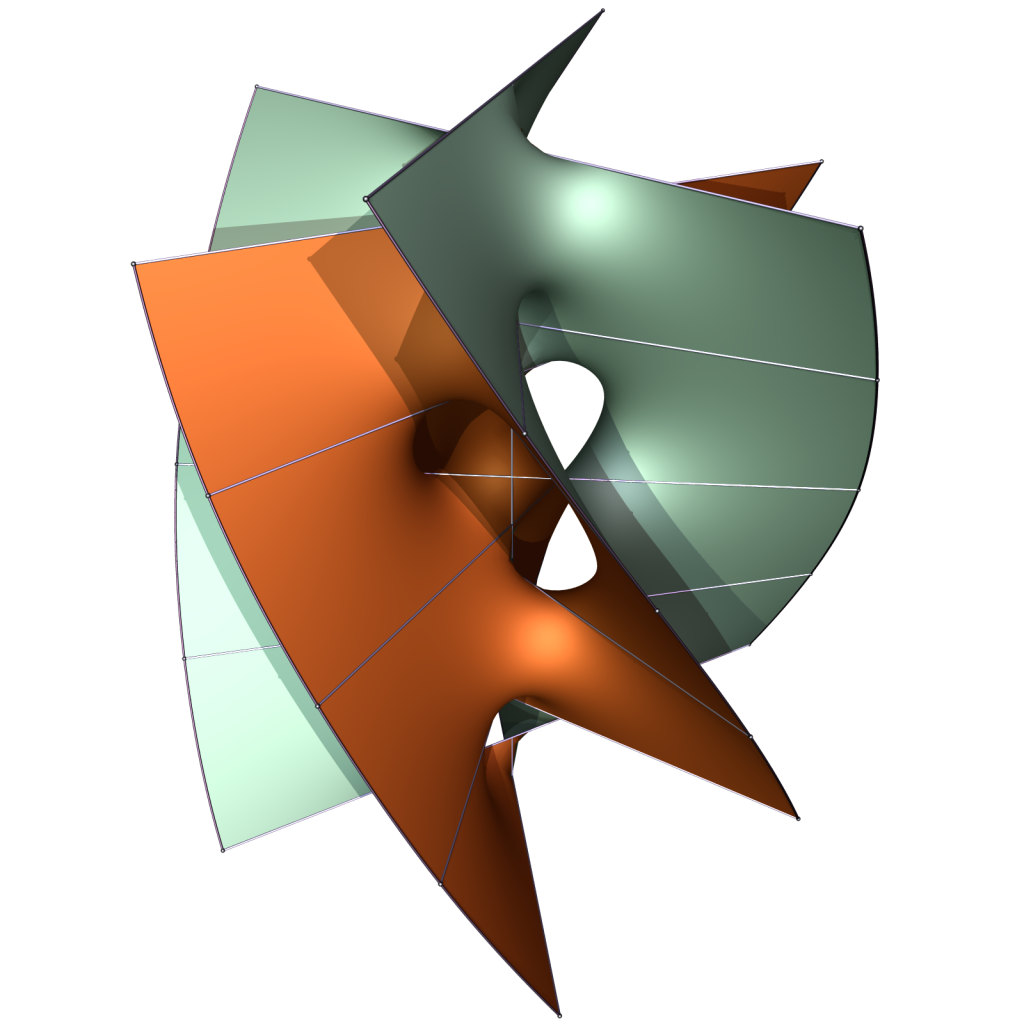

As these surfaces are chiral, twisting them counterclockwise leads to essentially different surfaces. In this case, the limit parking garage structure consists of three helicoidal columns with axes placed on a straight line. So during this entire deformation, two of the helicoids have magically cancelled.

By varying angles and edge lengths of the fundamental piece, one can repeat this construction of the 6-ended Fischer-Koch surfaces and make surfaces with more ends. Above and below you see images of the 10-ended version, together with their twisted friends.

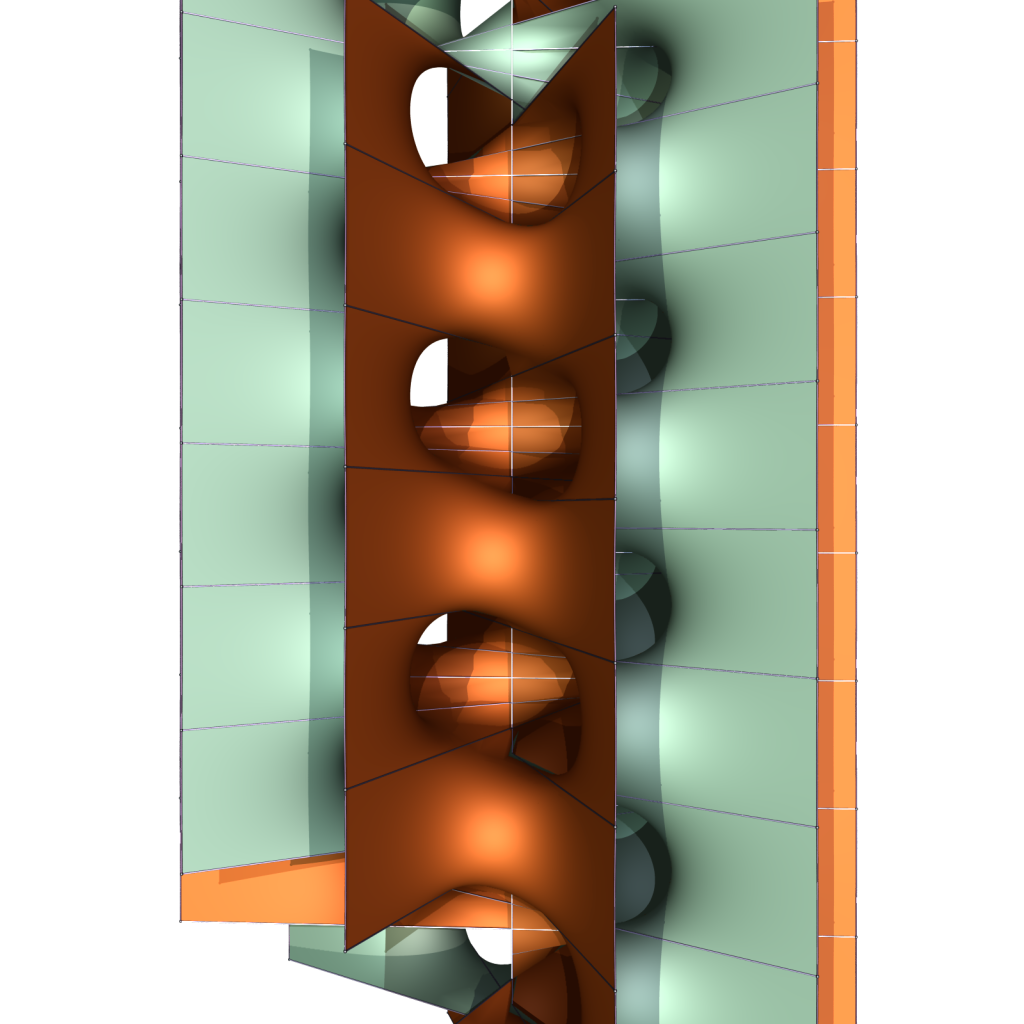

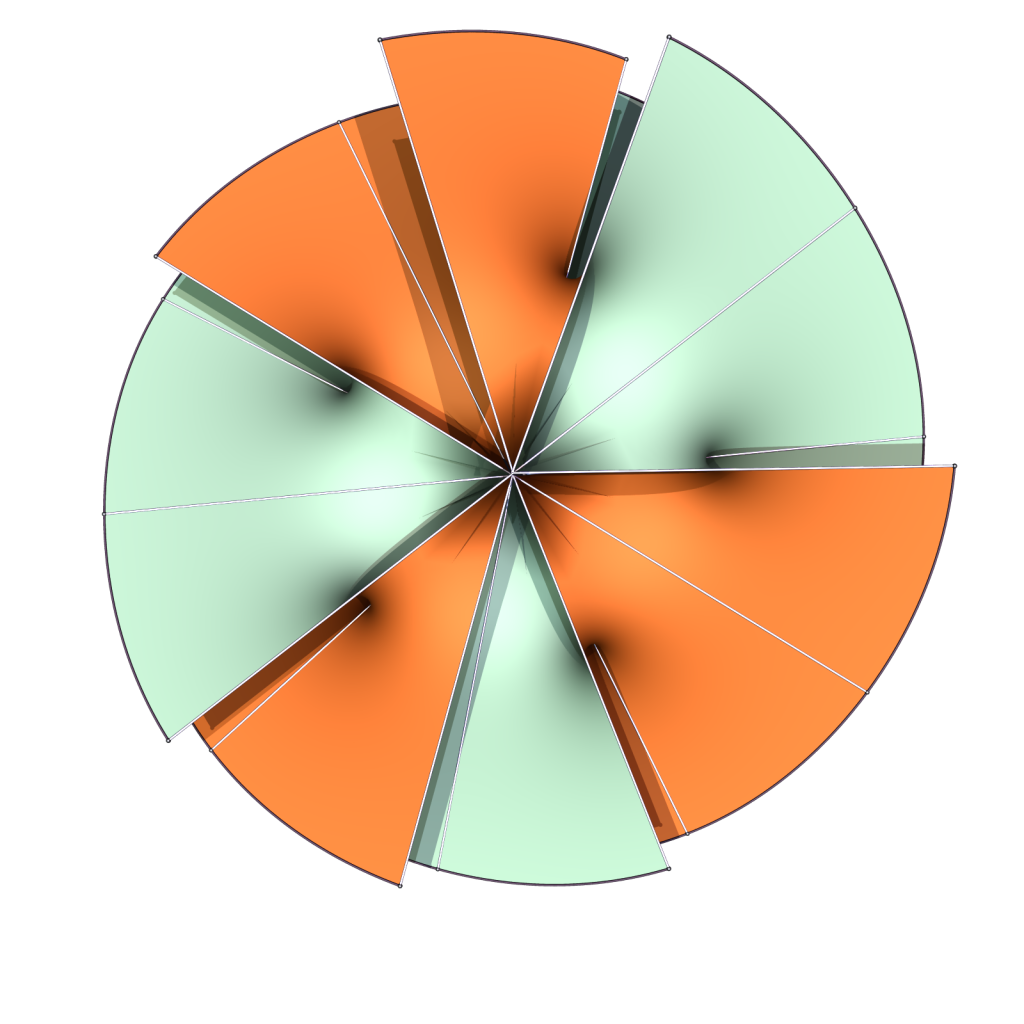
Again one obtains parking garage structures as limits, and the position of the helicoidal axes is indicated below: The case k=3 corresponds to last week’s surfaces, the case k=5 to the ones above. The colored disks represent helicoidal axes, with the color showing the different spins.

What about the case k=4, which should lead to 8-ended surfaces? Daniel Freese has shown that one can untwist the parking garage structures to screw motion invariant minimal surfaces:

and


But these surfaces can not be obtained using the Fischer-Koch construction. Below you see the completely untwisted version with annular ends.

One key difference to the Fischer-Koch surfaces is that opposing ends have opposite normals in Daniel’s surfaces (or differently colored sides, as visible above). If the vertical line was really a straight line, it would be a rotational symmetry line, and opposing ends had the same color.
So things are not always quite what they seem.