Here is a simple minimal surface of genus one, with two Enneper ends and with the three coordinate planes being symmetry planes.
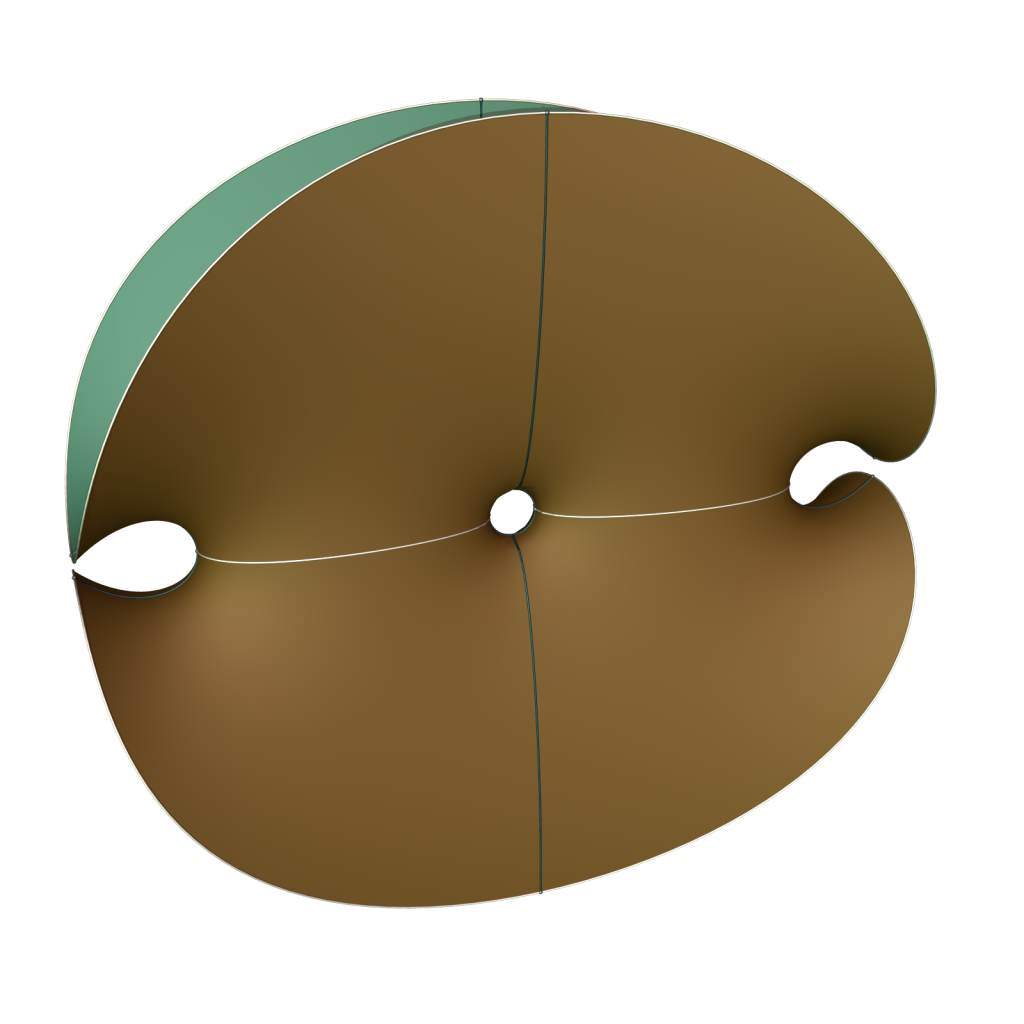

It comes in a 1-parameter family. One can parametrize one eighth of it in the upper half unit disk using the Weierstrass data and and
. Here a and b are real parameters varying between 0 and 1, and there is one period condition that can be used to determine a in terms of b.
One can create more symmetric versions of this surface, of genus n with two Enneper ends of higher order. Below are examples with n=3 and n=12.


Again the surfaces come with two parameters and one period condition, illustrated below with two surfaces for n=5:


The Weierstrass data generalize with small changes: and
, where
.
The period condition is unpleasant as it involves integrands with fractional exponents, leading to elliptic integrals, and worse : )


What happens when we increase the dihedral symmetry? When ,
, and in the Weierstrass data the fractional exponents disappear. This means that one can evaluate the period condition using residues, and this allows to determine
quite explicitly.
Moreover, one can use the implicit function theorem that the period problem has solutions for large values of n, without evaluating any integrals.
This method has been used by Ramazan Yol in his thesis and a recent preprint to give very simple and elegant existence proofs for many more minimal surfaces of high dihedral symmetry.
All this might sound unsatisfactory: Isn’t it the case that one can always increase the dihedral symmetry of a minimal surface? This has long been the general belief, but there are examples where this fails, rather dramatically.