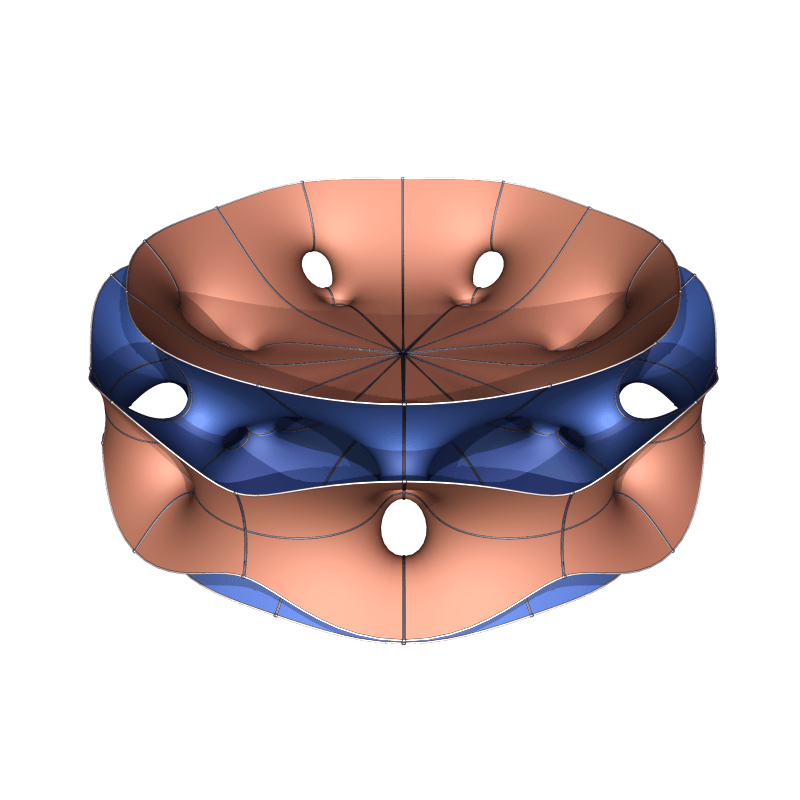
An attempt to disprove the Hoffman-Meeks conjecture was a surface of genus one by Hermann Karcher with four catenoidal ends that can be thought of as two coaxial catenoids stitched together. (Un?)fortunately, the surfaces obtained this way are not embedded.
Trying to add more handles by doubly stitching them doesn’t help either. One again obtains a 1-parameter family of such surfaces. Variations with higher dihedral symmetry are also possible:
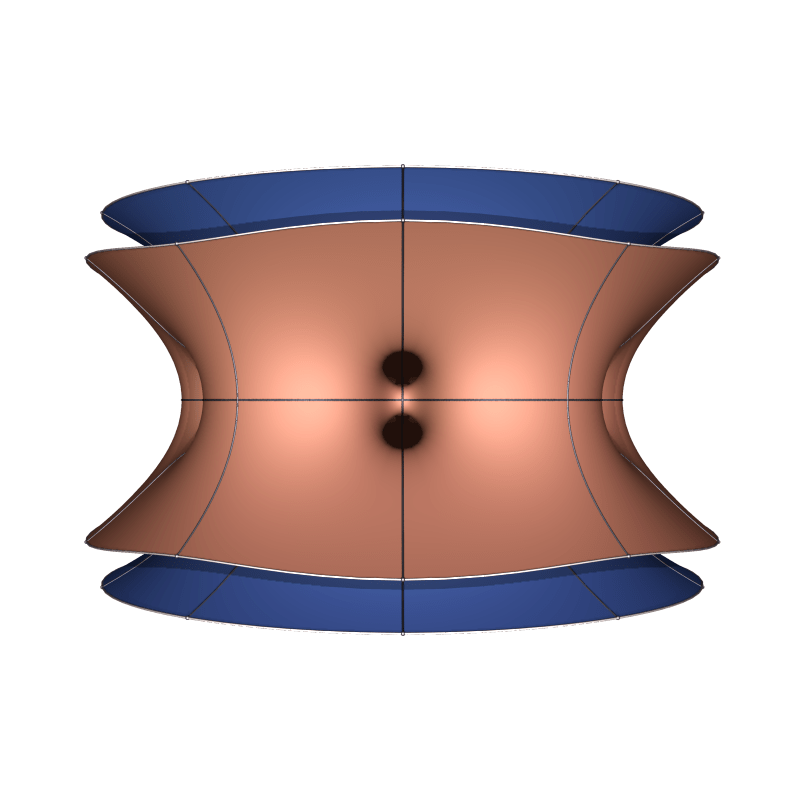
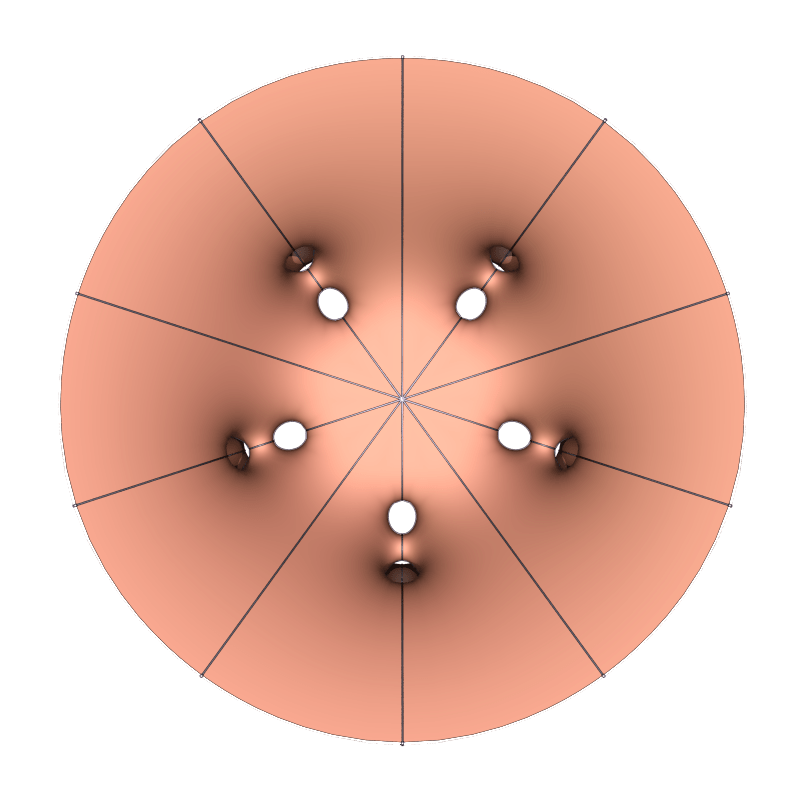
The period problem is 5-dimensional, and the existence has so far only been established numerically.
Minimal Surfaces 