In their paper Minimal surfaces in a Wedge of a Slab, Francisco López and Franscisco Martín construct a curious translation invariant minimal surface with planar ends:

It is neither embedded nor orientable. The only self-intersection happens along the z-axis, and one can think of it as solving a Plateau problem in a wedge of a slab, as the title of their paper suggests. The periodic surface resembles the Callahan-Hoffman-Meeks surface, which also have planar ends and horizontal straight lines.
Is it possible to replace a neighborhood of the z-axis by a singly periodic Scherk surface, thus creating an embedded surface with planar ends different from the Callahan-Hoffman-Meeks surface or their higher genus variations?
As Paco Martín has observed, the slab surface is related to the translation invariant helicoid with handle: If you don’t solve the vertical period condition for the latter, you obtain a 1-parameter family of surfaces that slides the surface along the z-axis:




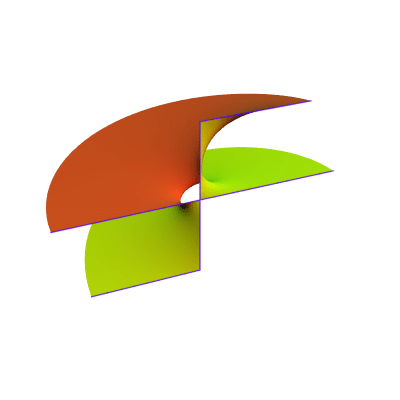
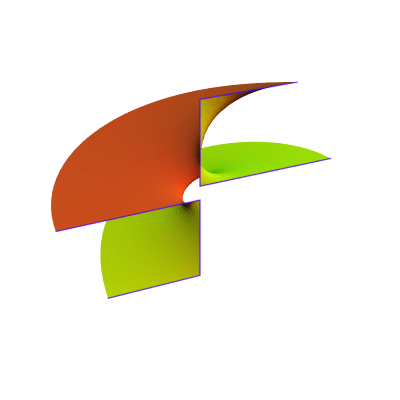
The first image above is half of the slab surface, and the fifth is half of the translation invariant helicoid with handle.
Resources
Mathematica Notebook
PoVRay Sources