In 1997, Nicos Kapouleas published a paper in which he constructed finite total curvature embedded minimal surfaces with an arbitrary number of ends. He did this by taking the union of catenoids and planes with the same axis of symmetry, and desingularizing their circular intersections by bent singly periodic Scherk surfaces.

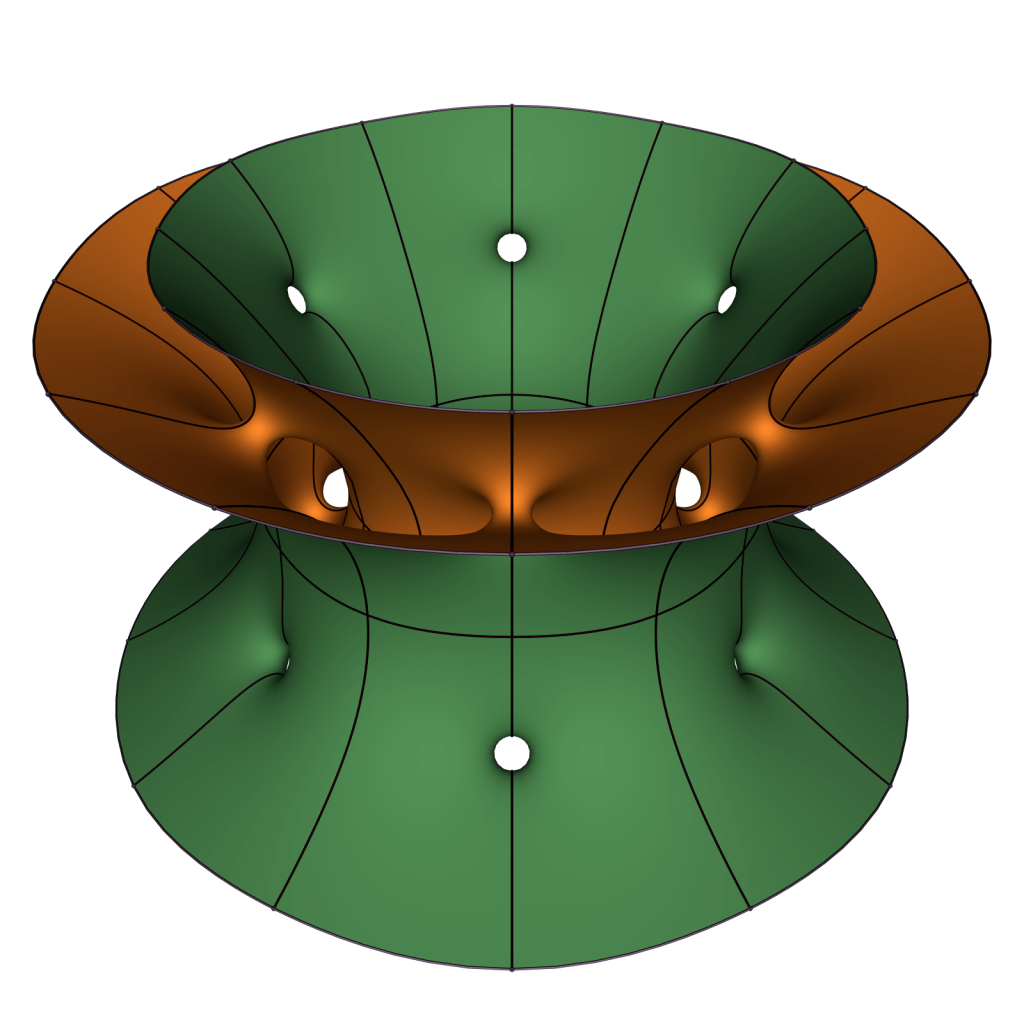
Above are two examples with 6-fold dihedral symmetry that desingularizes the intersection of just two catenoids. One needs to make sure that the growth rates of the two catenoids don’t prevent the surface to be embedded.
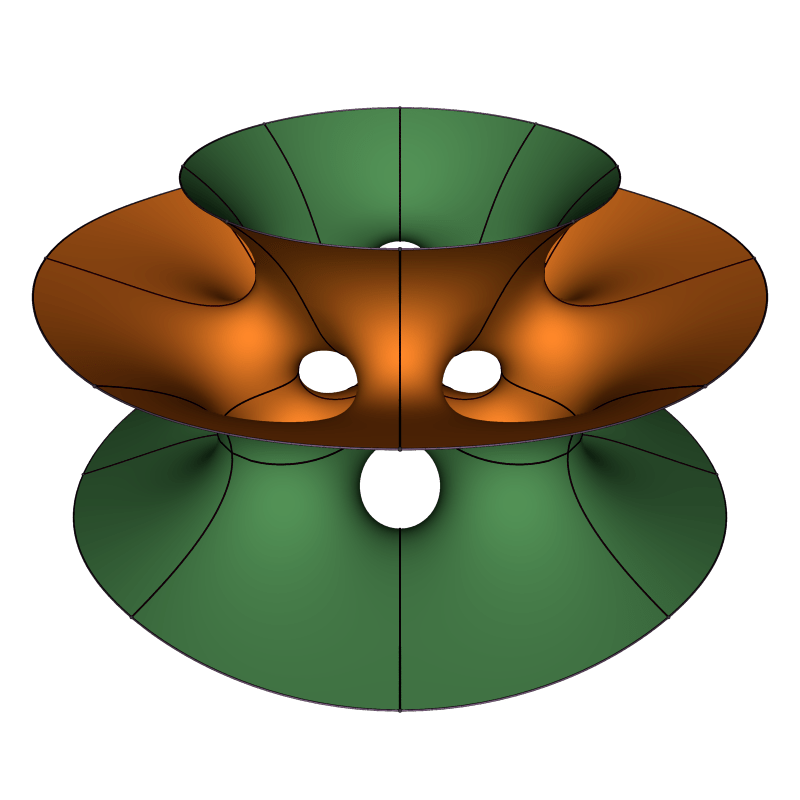



Amusingly, the 3-dimensional period problem often has two solutions for the same pair of catenoidal growth rates. For smaller dihedral symmetry it becomes harder and harder to make the surfaces embedded.
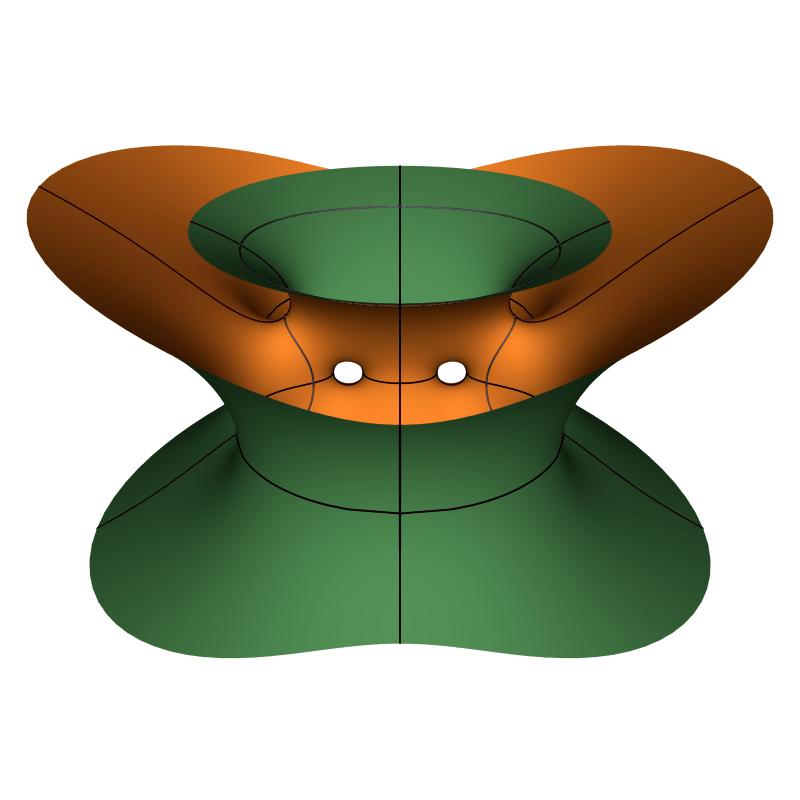

For 2-fold symmetry we believe there are no embedded examples, the first ones exist for 3-fold symmetry. All period problems here have been solved numerically, so there is no simple existence proof for these surfaces yet.
Resources
Mathematica Notebook by Ramazan Yol
Related Surface: Tori with four catenoidal ends