Similar to the k-Noids with k handles one can add handles to the singly periodic Karcher-Scherk surfaces that pull the ends together in pairs:

These surfaces (with their dihedral symmetry) come in a 1-parameter family that simultaneously changes the angle between the ends and the location of the handles.

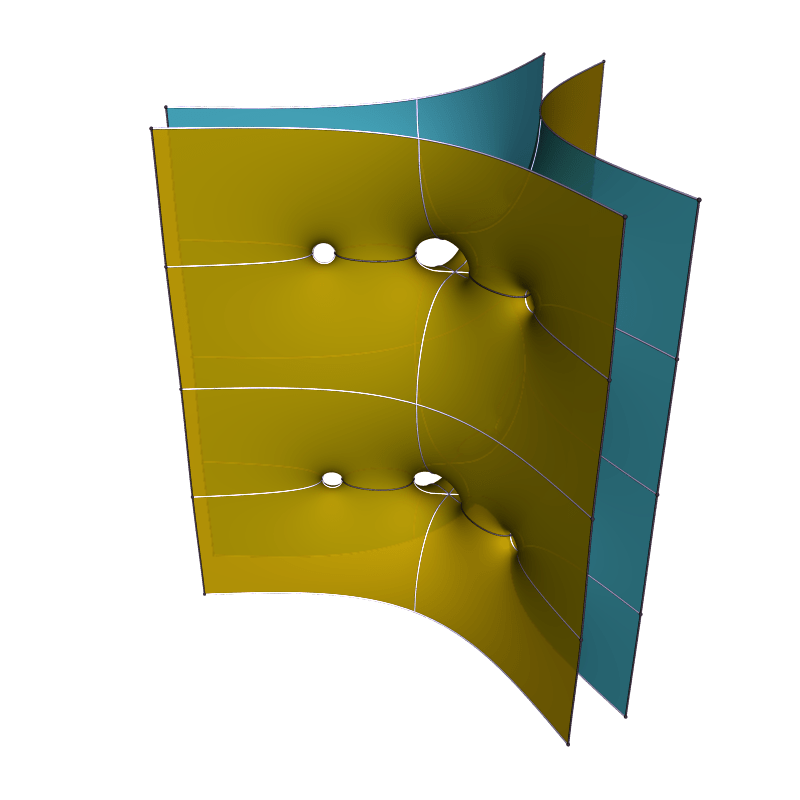
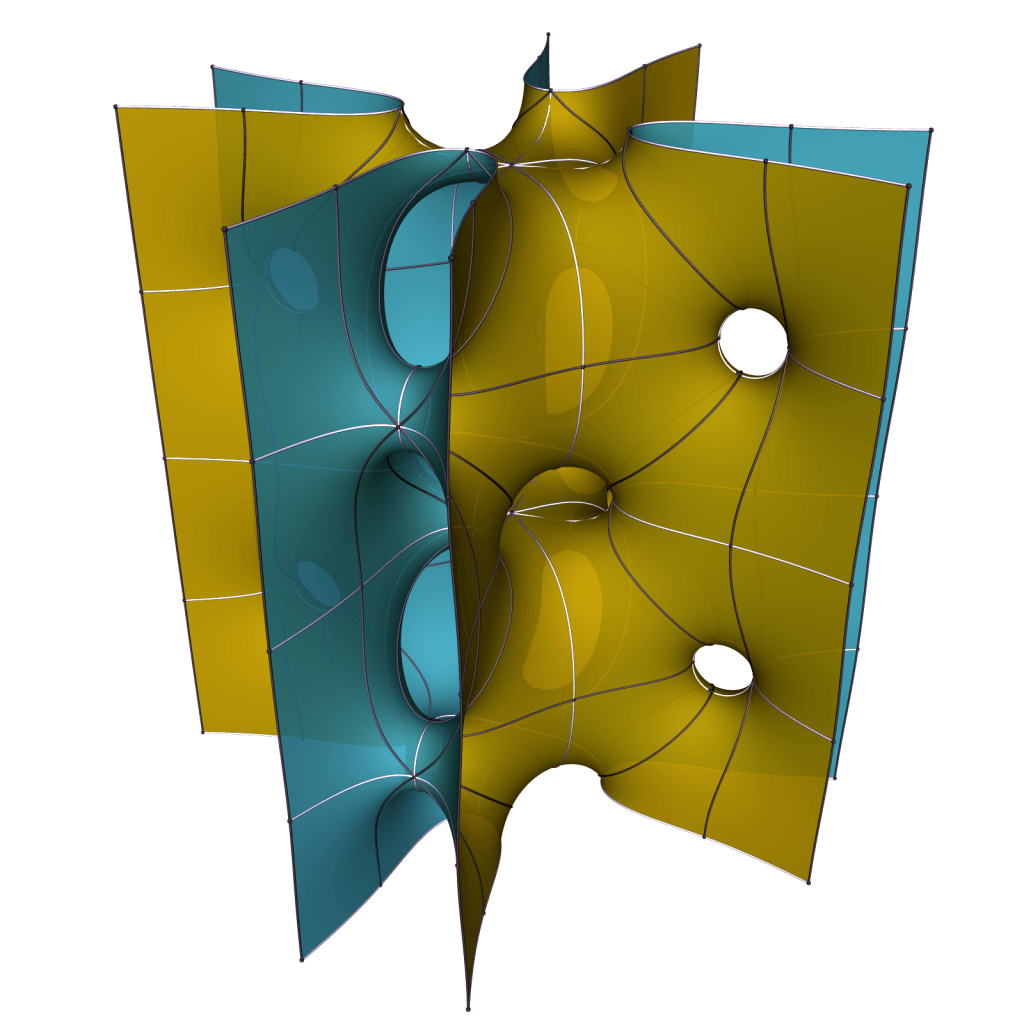
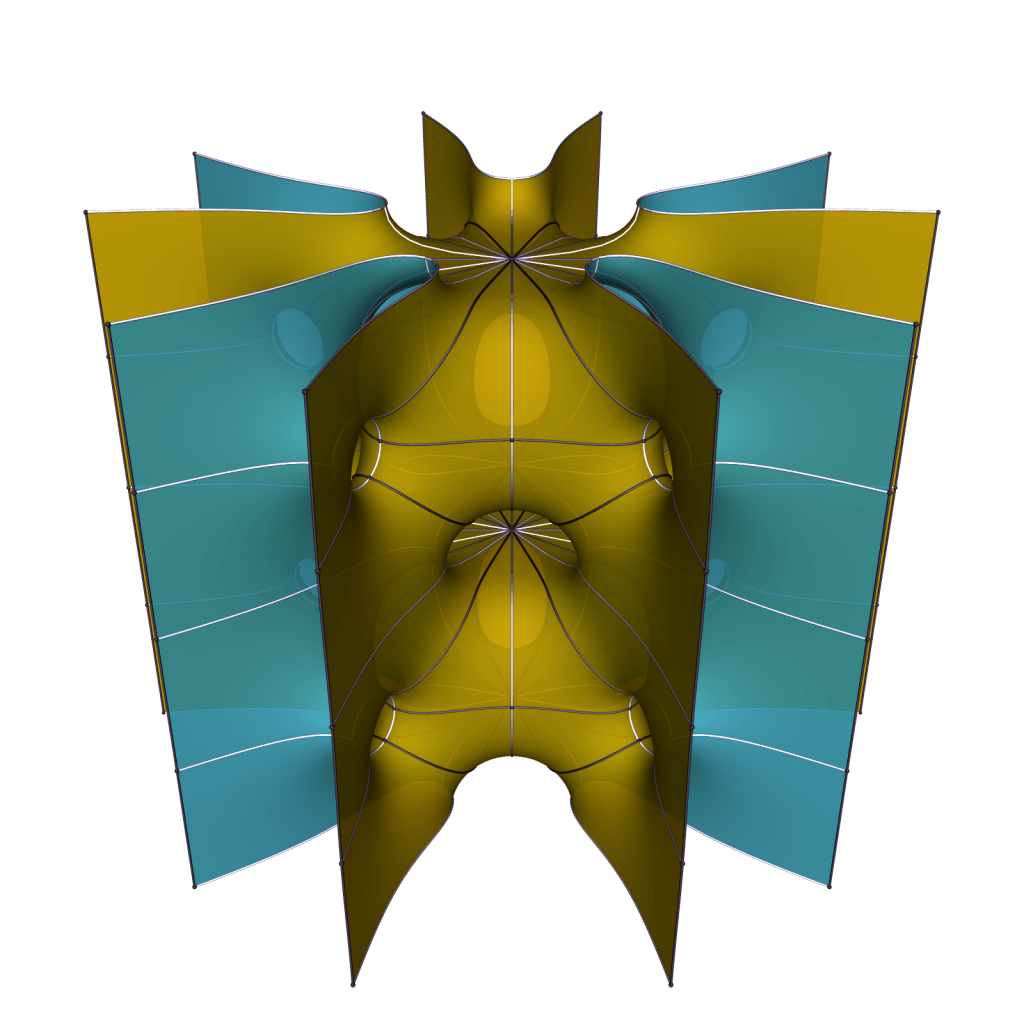
Above two examples for k=3 and below for k=4. Not all members of a family are embedded, as the annular ends can well intersect.
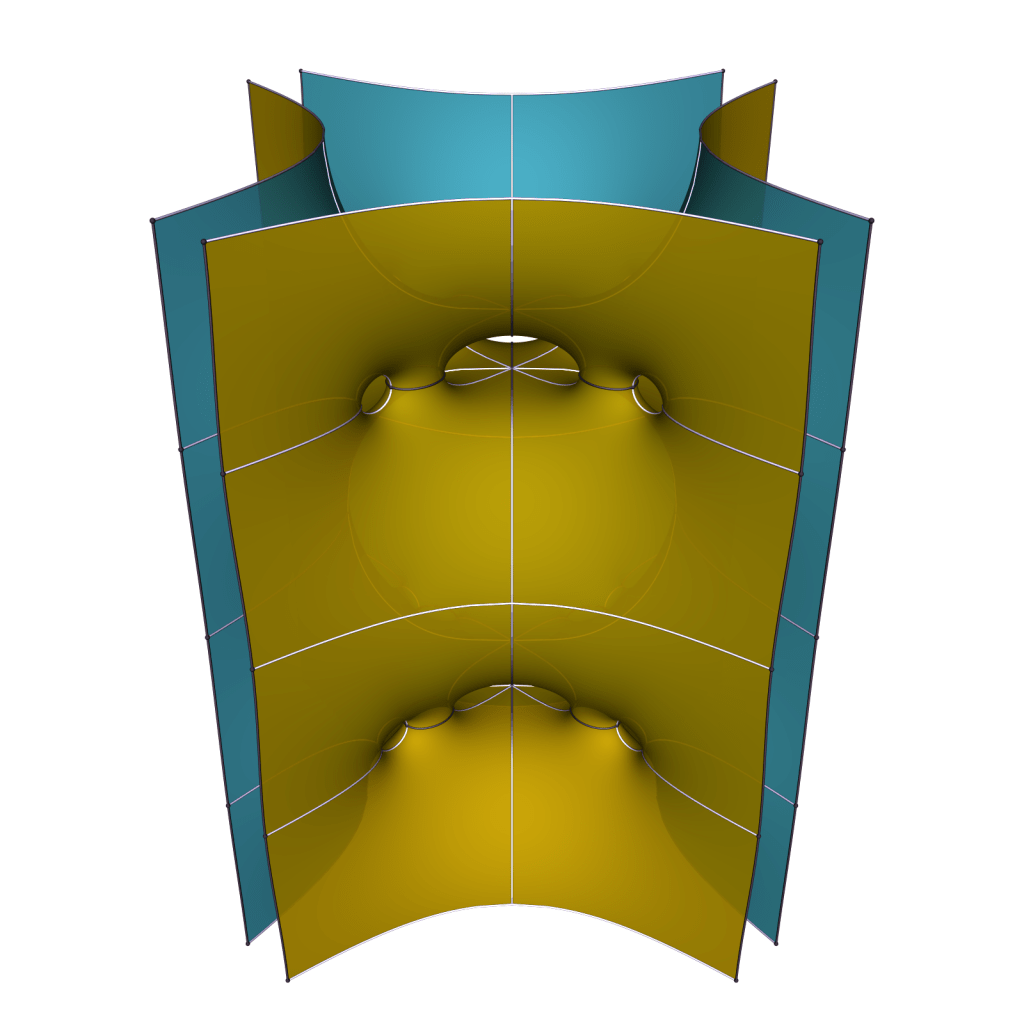
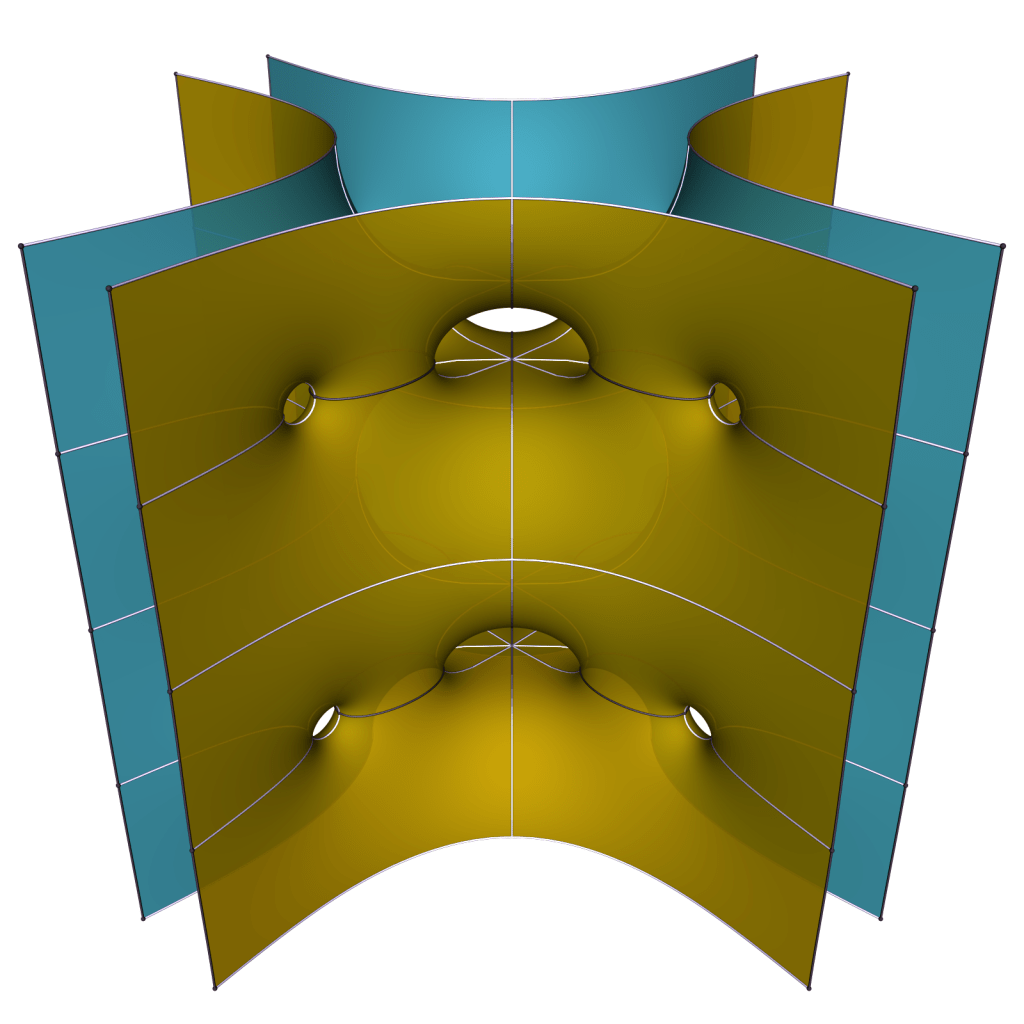
If we keep the annular ends parallel in pairs, these surfaces will converge for increasing k to the doubly periodic Karcher-Scherk torus. Ramazan Yol has given an existence proof in his thesis for large values of k, using the implicit function theorem at this limit.
Surprisingly, there is (at least) one more way to add handles a half period apart:
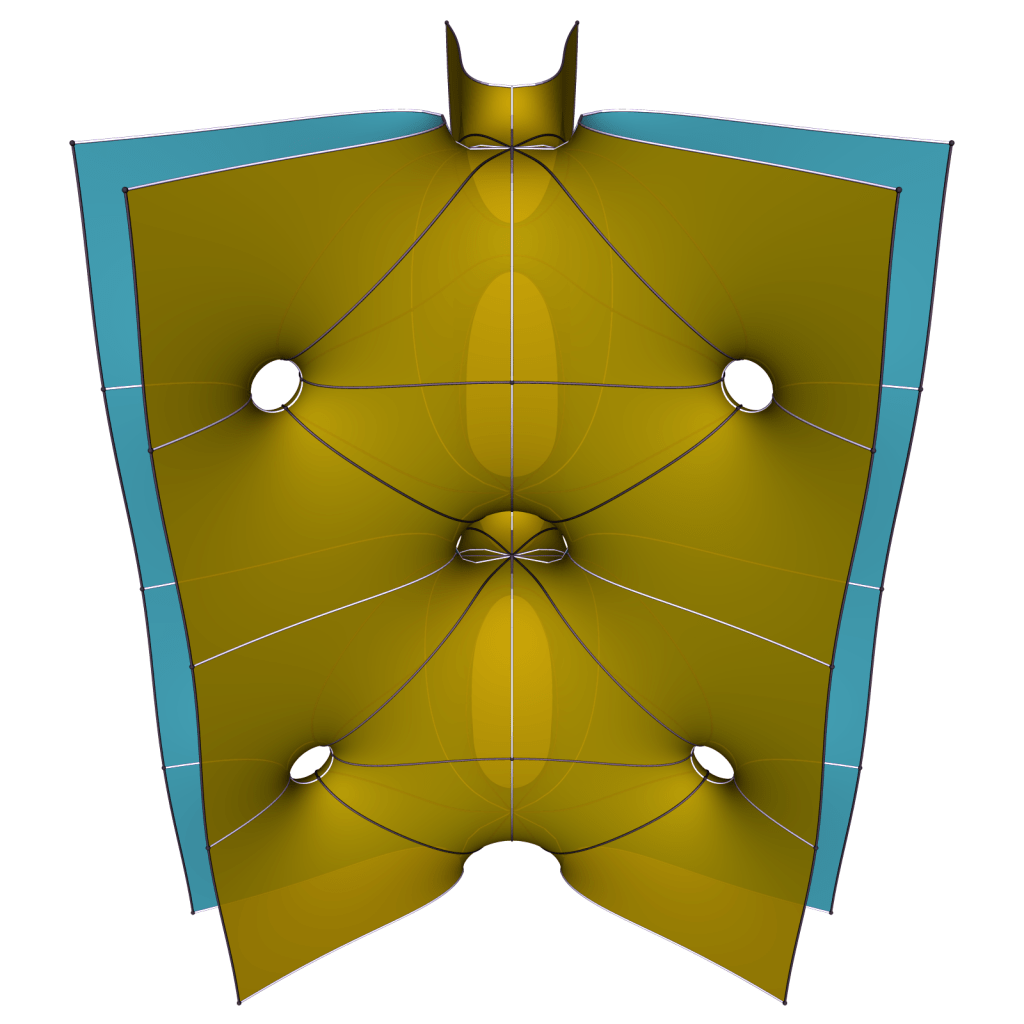
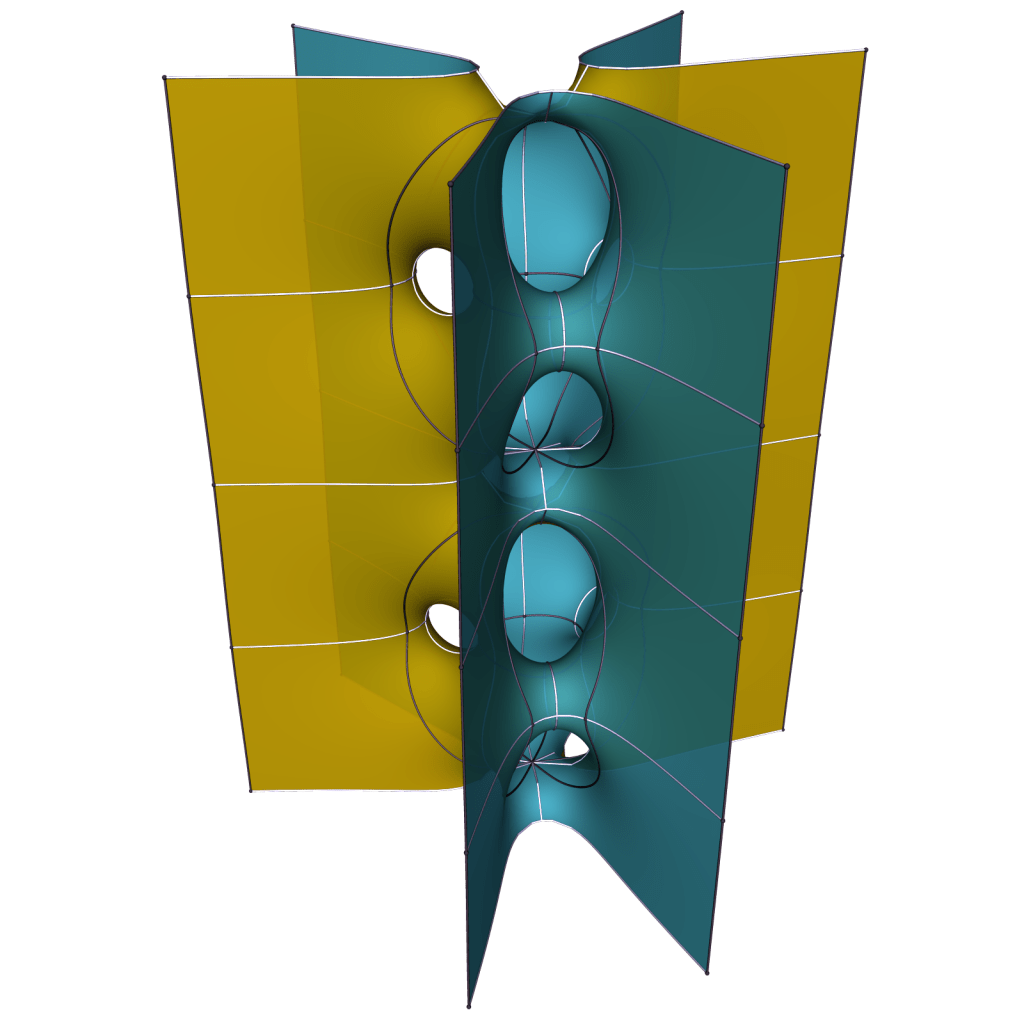
It doesn’t seem possible to make the ends parallel in pairs, so we expect the limit for k to ∞ to be a doubly periodic surfaces of genus one that is never embedded.
Resources
Mathematica notebooks for standard case and exotic case (by Ramazan Yol)
PoVRay sources for standard case and for exotic case