The construction of minimal surfaces on tori (or on Riemann surfaces of higher genus) usually requires to close periods that are not just residues. If this doesn’t work, one obtains periodic surfaces. A simple example is the catenoid with a handle, which does not exist as a closed surface.
Attempting to grow a handle inwards necessarily leaves a gap. This is a consequence of a theorem of Richard Schoen: Every complete, properly immersed minimal surface with two catenoidal ends is the catenoid. Incidentally, a proof of this using the Enneper-Weierstraß representation might provide new insights.
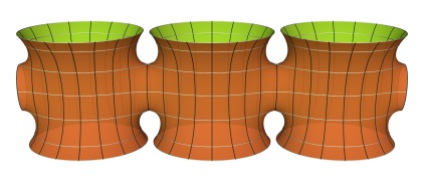
If the handle is grown outwards, one obtains a more appealing version which Hermann Karcher calls a Fence of Catenoids in his Tokyo notes. With varying parameter, the catenoidal neck either becomes smaller, or the surfaces converge apparently to the double of a planar surface, similar to what happens to the torus with two Enneper ends. This behavior has not been studied, as far as I know.
Resources
Mathematica Notebook inwards and outwards
PoVRay Sources inwards and outwards
Related Surfaces
- Torus with Two Enneper Ends
- Symmetrizations
- Hackman Surfaces