While the singly periodic Scherk surface has been quite amenable to modifications and variations, its doubly periodic sibling has been rather stubborn. It resisted initial attempts to add handles between the annular ends, until Hermann Karcher succeeded by doing so between every other layer.
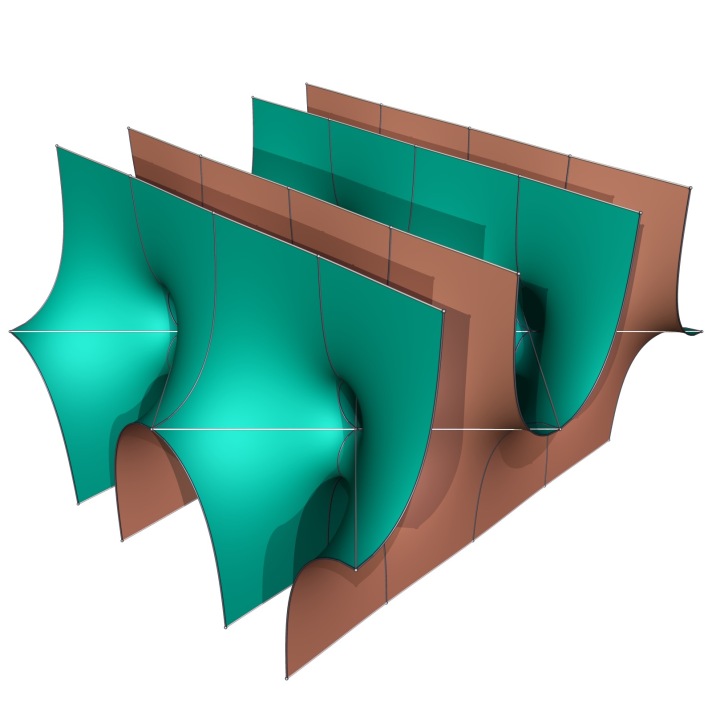
The surface maintains most symmetries, including the horizontal straight lines (but loses the vertical ones). The attracting force exerted by the catenoidal necks can be best seen in a top view:

Like the original Scherk surface, one can change the angle between the annular ends, as shown by Frank Baginski and Valerio Ramos-Batista and independently by Casey Douglas. One can also add more handles, as shown by Matthias Weber and Michael Wolf.
An open question is whether one can add fewer handles: The holy grail would be a genus one Scherk surface, with just one handle (and no periodicity). Less ambitious but still very interesting would be a periodic surface of genus one with more than two orthogonal top and bottom ends.
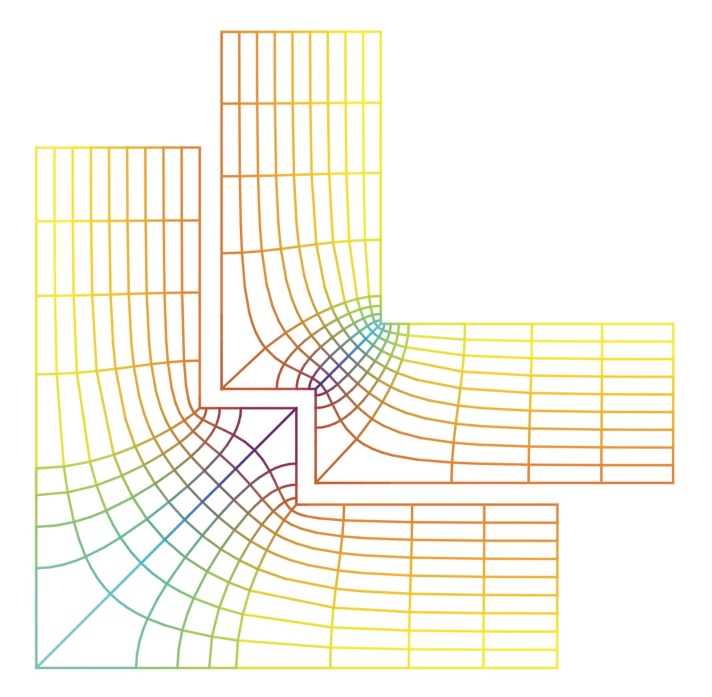
The flat structures of G dh and 1/G dh show a strong resemblance to those of the Chen-Gackstatter surface. The period condition can again be stated as the two domains fitting together and being conformal by a vertex preserving map.
Resources
D. Hoffman, H. Karcher, and F. Wei. The genus one helicoid and the minimal surfaces that led to its discovery. In Global Analysis and Modern Mathematics. Publish or Perish Press, 1993. K. Uhlenbeck, editor, p. 119–170
PoVRay Sources
Related Surfaces
- Doubly Periodic Scherk Surface
- Sheared Karcher-Scherk Surfaces
- Translation Invariant Genus One Helicoid
- Karcher Scherk surfaces of higher genus