Ernst Lebrecht Henneberg (1850-1933) wrote his dissertation in 1875 under Hermann Amandus Schwarz. An excerpt appeared 1876 in the Quarterly Journal of the Natural Research Society in Zürich under the title Ueber diejenige Minimalfläche, welche die Neil’sche Parabel zur ebenen geodätischen Linie hat.
The paper discusses a special case of the problem to determine a minimal surface that has a given planar curve as a geodesic, the planar curve being Neil’s parabola. Today this problem would be considered a special case of the Björling problem.

The Henneberg surface can be given by the Weierstrass data G(z)=z and dh=z\left(1-\frac1{z^4}\right). There are punctures at 0, \infty, and the fourth roots of unity.

Because the height differential is invariant under z\mapsto 1/z, it is enough to consider the surface on the unit disk, where it parametrizes a projective plane. The puncture at 0 represents an Enneper end:

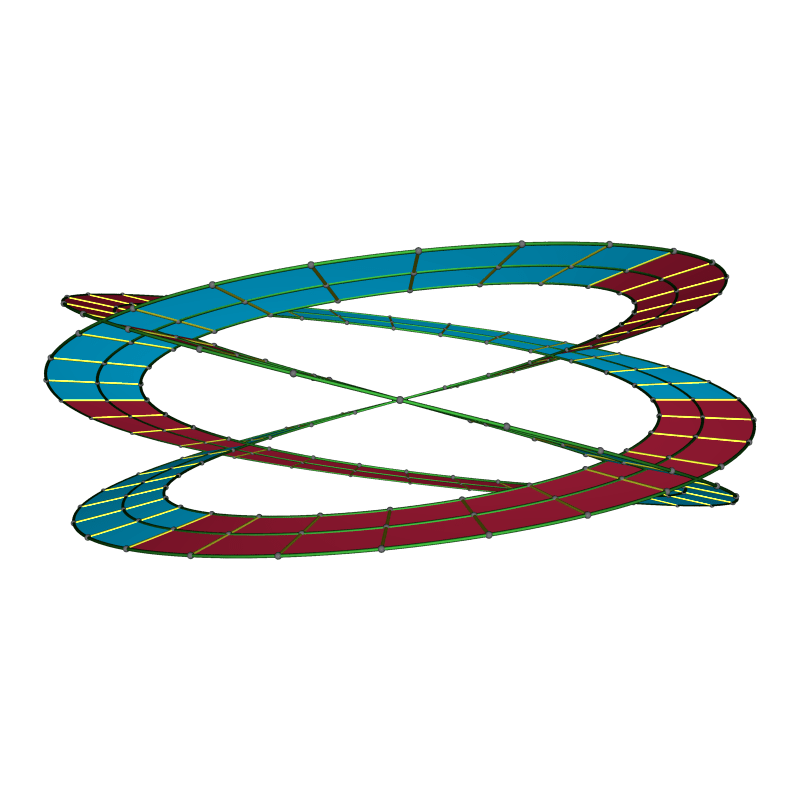
To better understand the surface, we assemble it from pieces bounded by symmetry lines. Below is the top half, containing one of the crosscut singularities and half of the vertical segments as well as the pair at horizontal lines in the plane z=0.

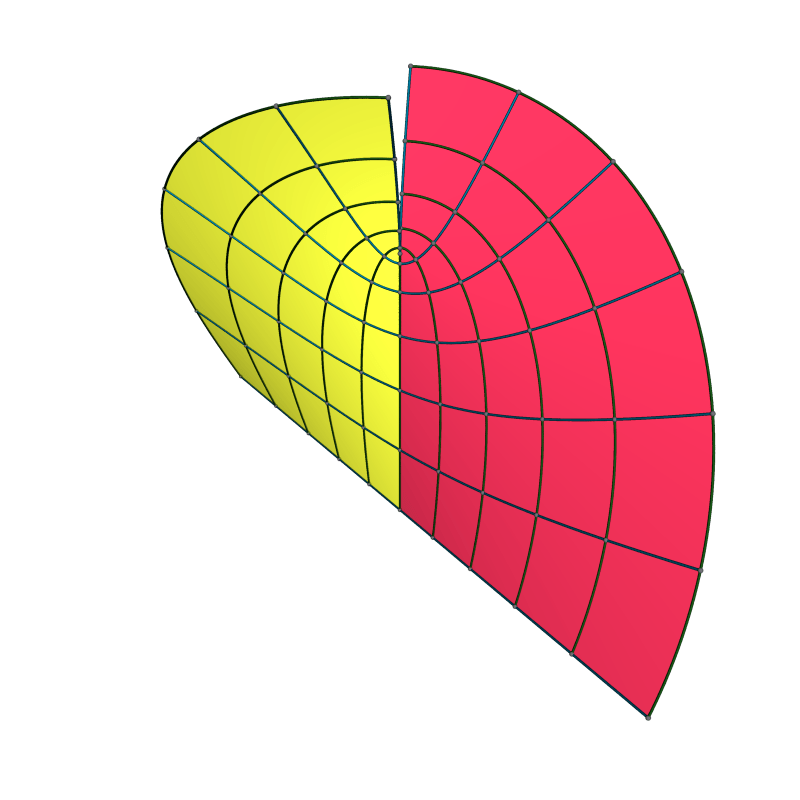
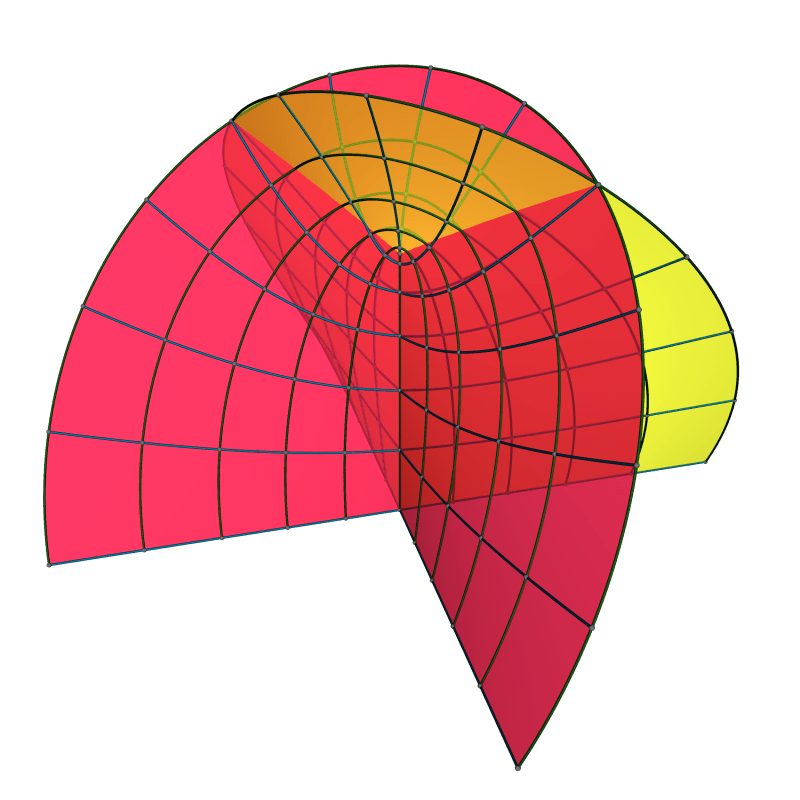
Completing the surface by doubling it and then showing more of the end:

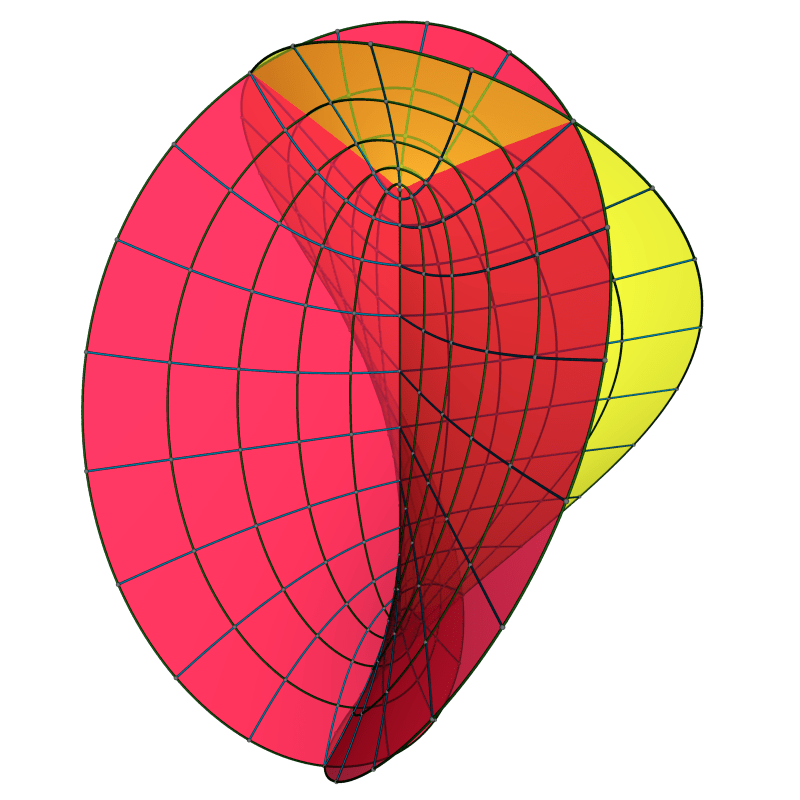
A straightforward generalization of the Henneberg surface increases the dihedral symmetry. We use as Weierstrass data G(z)=z^k and dh = z^k\left( 1- \frac1{z^{2k+2}} \right)\, dz. The Henneberg surface corresponds to k=1. Below is the surface for the next complicated case k=2:

Resources