A 1-Noid is a minimal surface with only one catenoidal end. The maximum principle prevents 1-Noids to exist in R3 to exist, but one can have them as quotients of screw-motion invariant singly periodic surfaces. The simplest example is the alternating fence of catenoids.
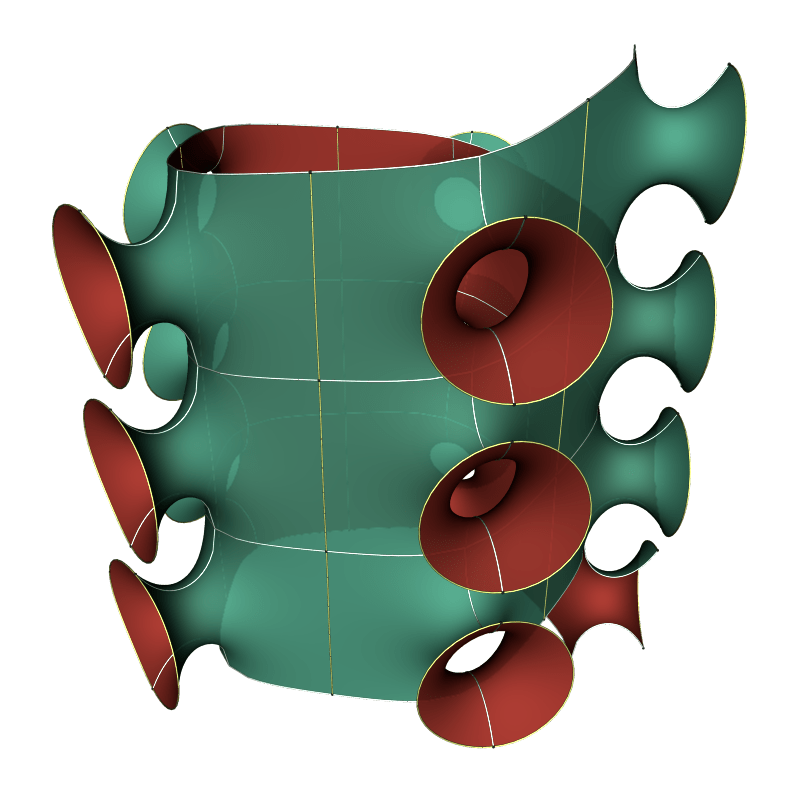
Michelle Hackman has constructed more general toroidal 1-Noids in her thesis. She proved that one can have such a 1-Noid on every conformal type of torus.
In the simplest case, a suitable power of the screw motion becomes a translation, making both the two-dimensional period problem easier to solve and the surface easier to render.
Above and below are examples where the power is k=5. For each power, there is (at least) a 1-parameter family of surfaces.
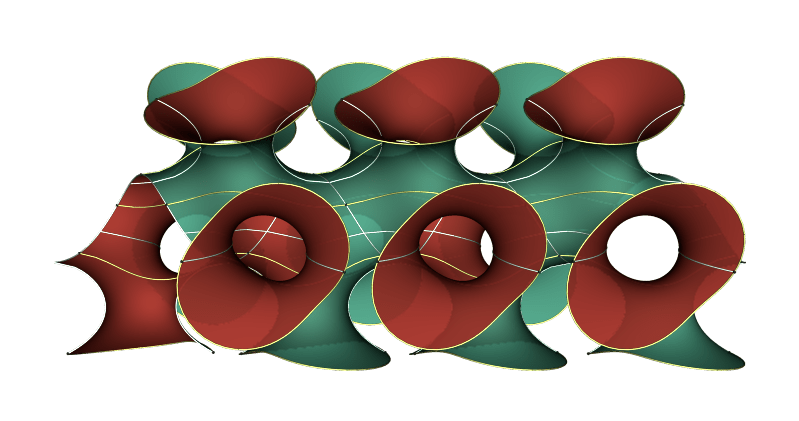
Below are two examples with k=3:
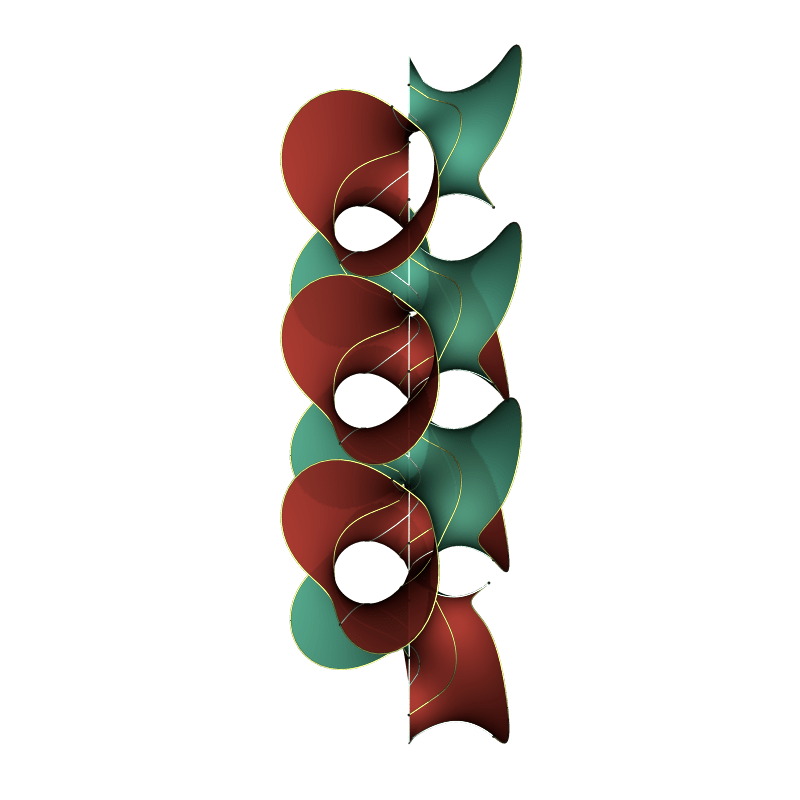
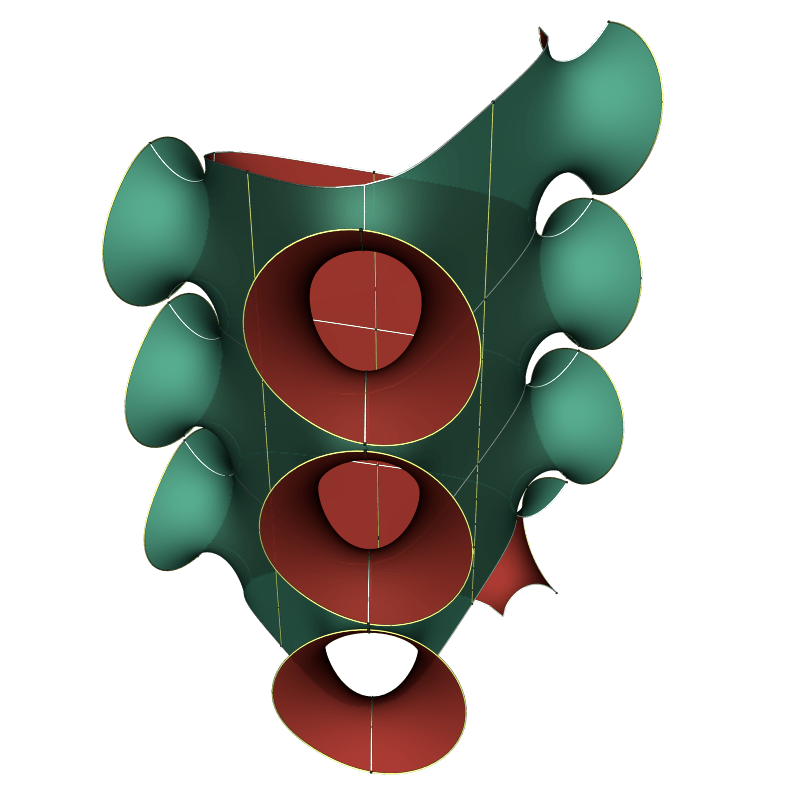
The parameter Michelle uses is the imaginary part of the lattice constant. For small parameter, the surfaces narrow down to their axis of screw motion, and the tori become less rectangular, making the catenoidal ends appear to be crooked. For large parameter values, the intersection of the surface with a horizontal plane seems to approach a regular k-gon.
It might be possible to classify the toroidal k-noids, but numerical experiments with small parameter values indicate that it won’t be simple.