The Fischer-Koch-Freese surfaces are 1-parameter families of screw motion invariant minimal surfaces of genus one and 2k ends in the quotient for every integer k>2. The cases of odd k reduces to the helicoidal Fischer-Koch surfaces. A special case arises when the helicoidal ends become annular Scherk-type ends, and the surfaces become translation invariant.
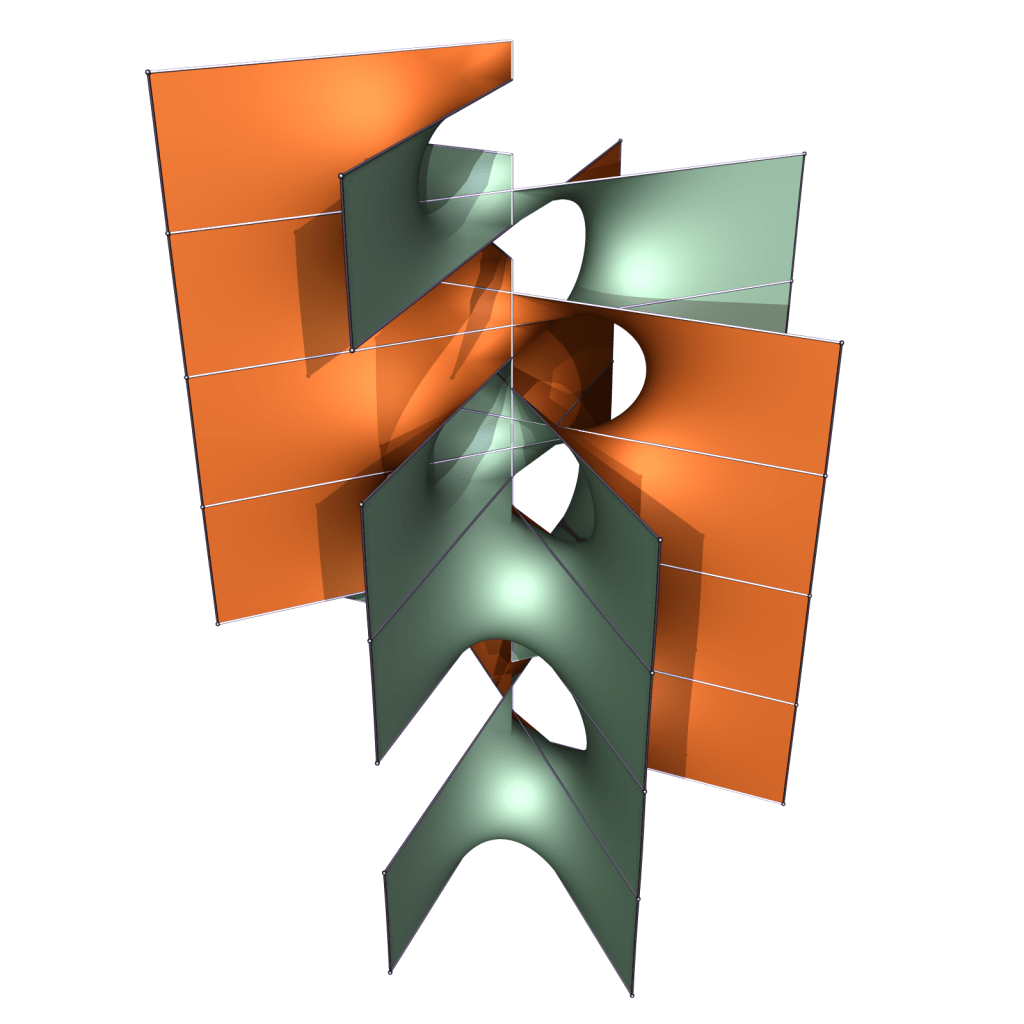
Above you can see a translation invariant surface with 8 ends and genus one in the quotient. It admits a deformation through screw motions either way, i.e. with positive or negative twist angles:


In the two limits, we obtain parking garage structures, i.e. foliations of R3 by horizontal planes with singular vertical lines representing helicoidal axes.
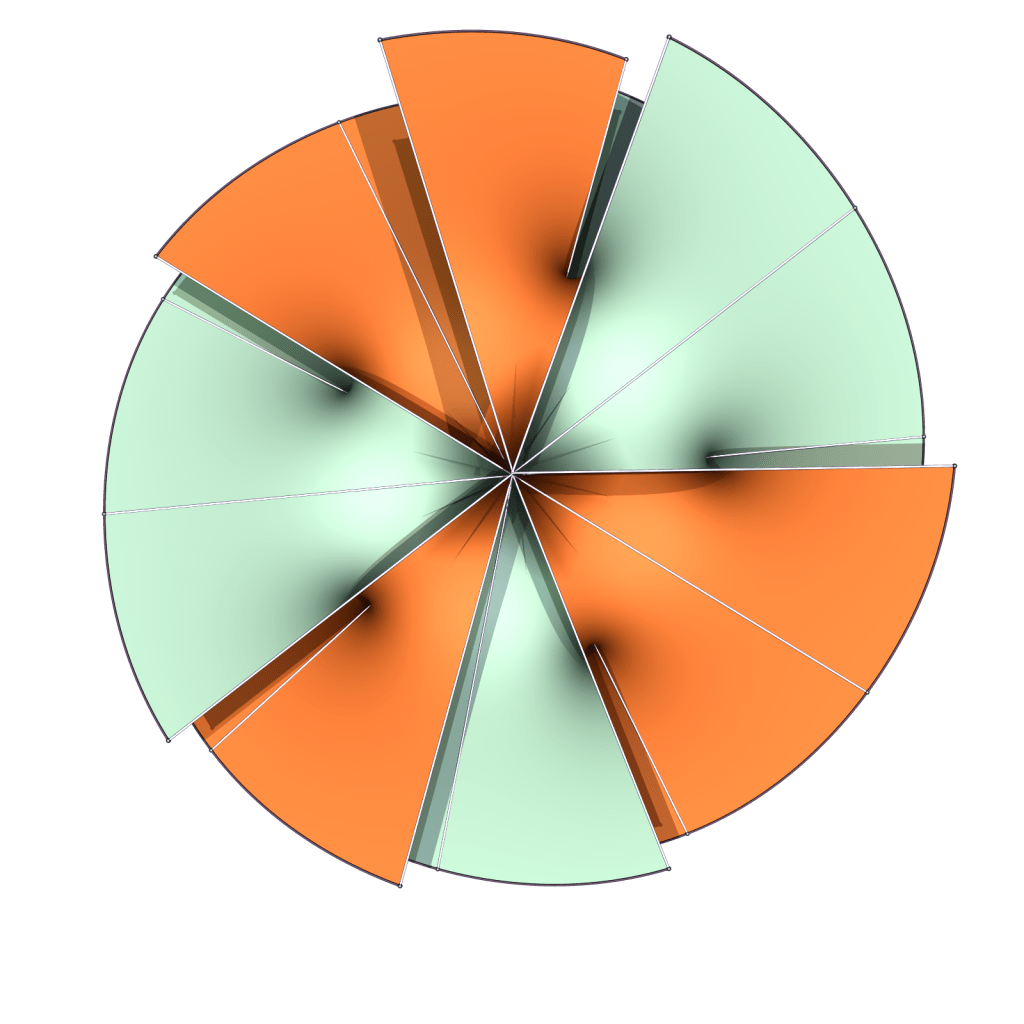
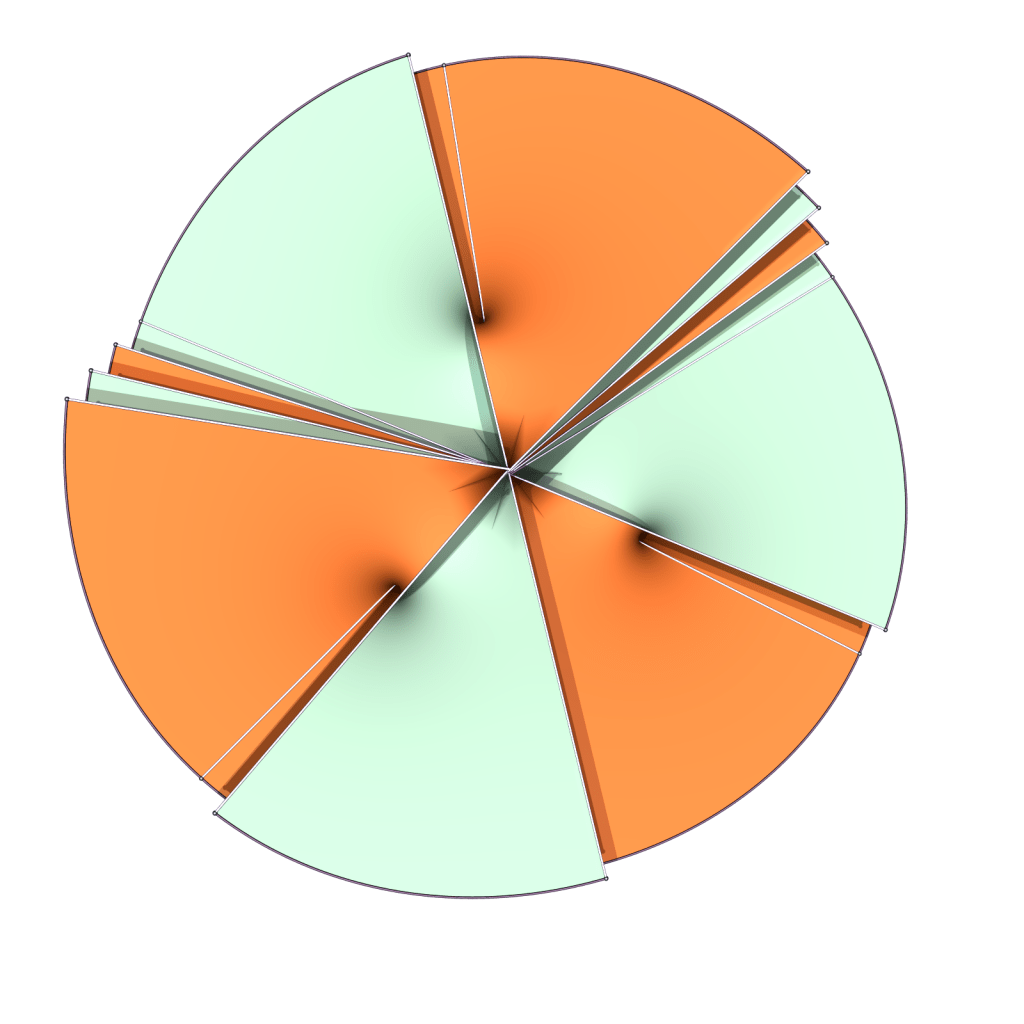
The limit on the left has three helicoids at the third roots of unity and one at the center, all with the same “spin”, while the limit on the right has five helicoids with the same spin at the fifth roots of unity and one with opposite spin at the center.
These surfaces cannot be obtained using the Fischer-Koch construction. One key difference to the Fischer-Koch surfaces for odd k is that opposing ends have opposite normals in Freese’s surfaces (or differently colored sides, as visible above). If what appears to be a vertical line was really a straight line (as in the odd k case), it would be a rotational symmetry line, and opposing ends had the same color.
Resources
Mathematica Notebook (by Ramazan Yol)