One can add any number of handles to the Callahan-Hoffman-Meeks surface. Informally, let’s denote by CHMr,s a translation invariant surface with 2r ends of genus s+1 in the quotient. The original Callahan-Hoffman-Meeks surface is then denoted by CHM1,1.
Below are images of the surfaces CHM1,2, CHM1,3, CHM1,4 and CHM1,5.

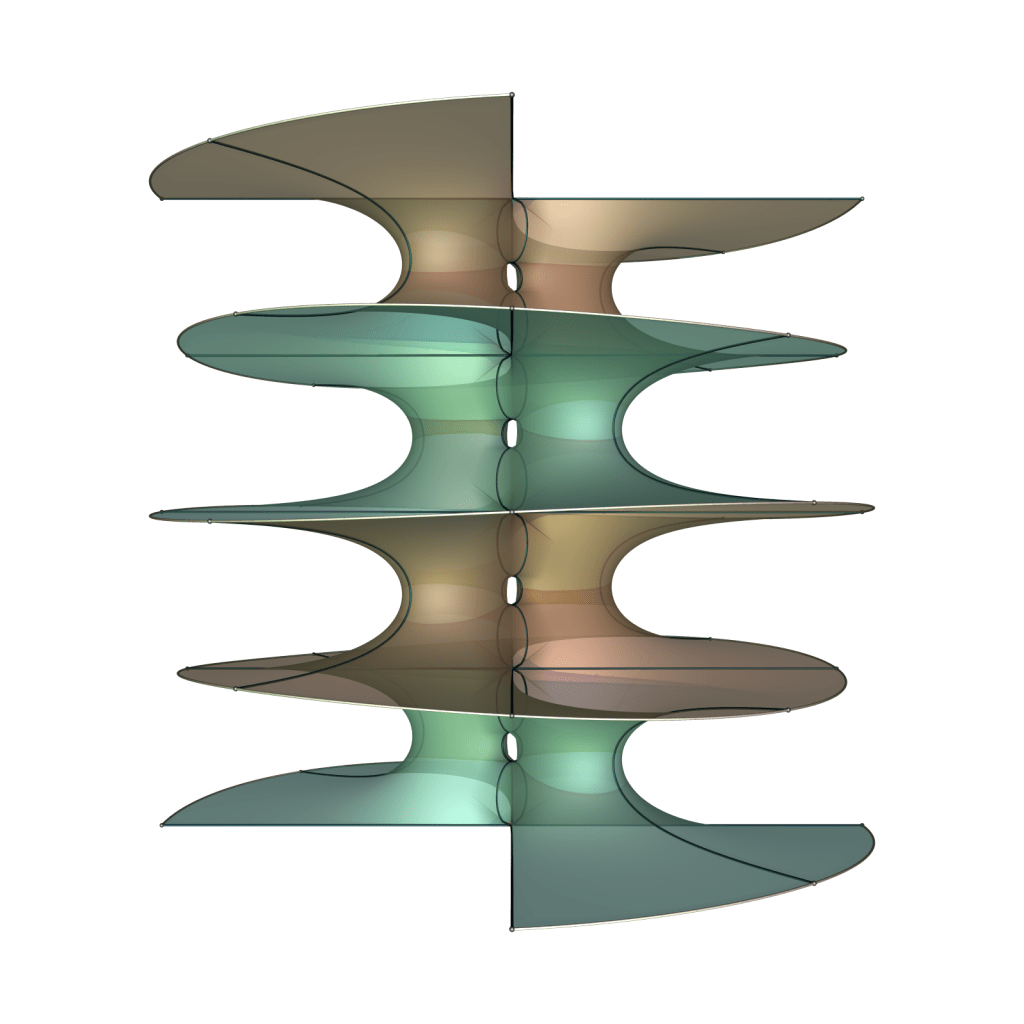
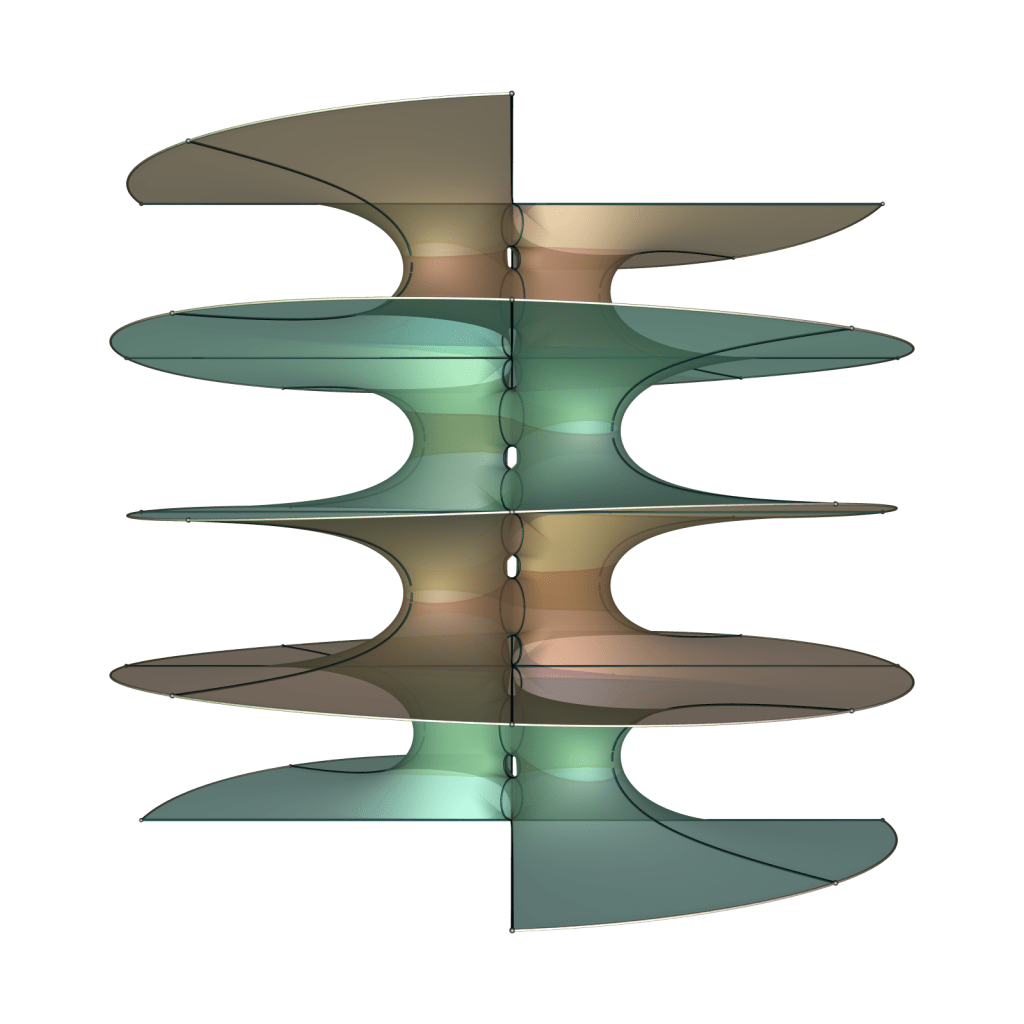
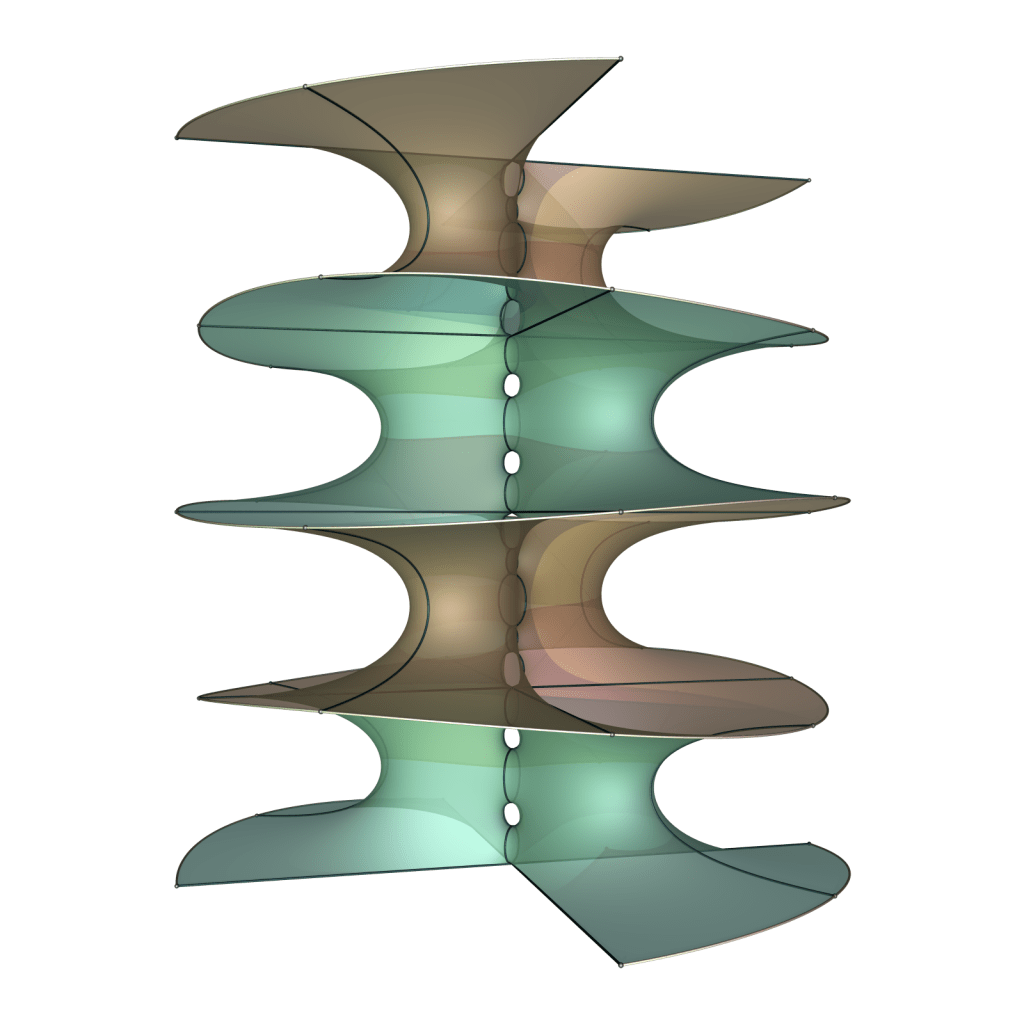
The surface CHM1,2 deserves special attention as the geometry of the handles at each end is exactly what the Horgan surface attempts. Note also that CHM1,3 could be called the singly periodic Wohlgemuth surface.
So far the examples have just two ends in a translational fundamental piece. Below are images of DH2,3:
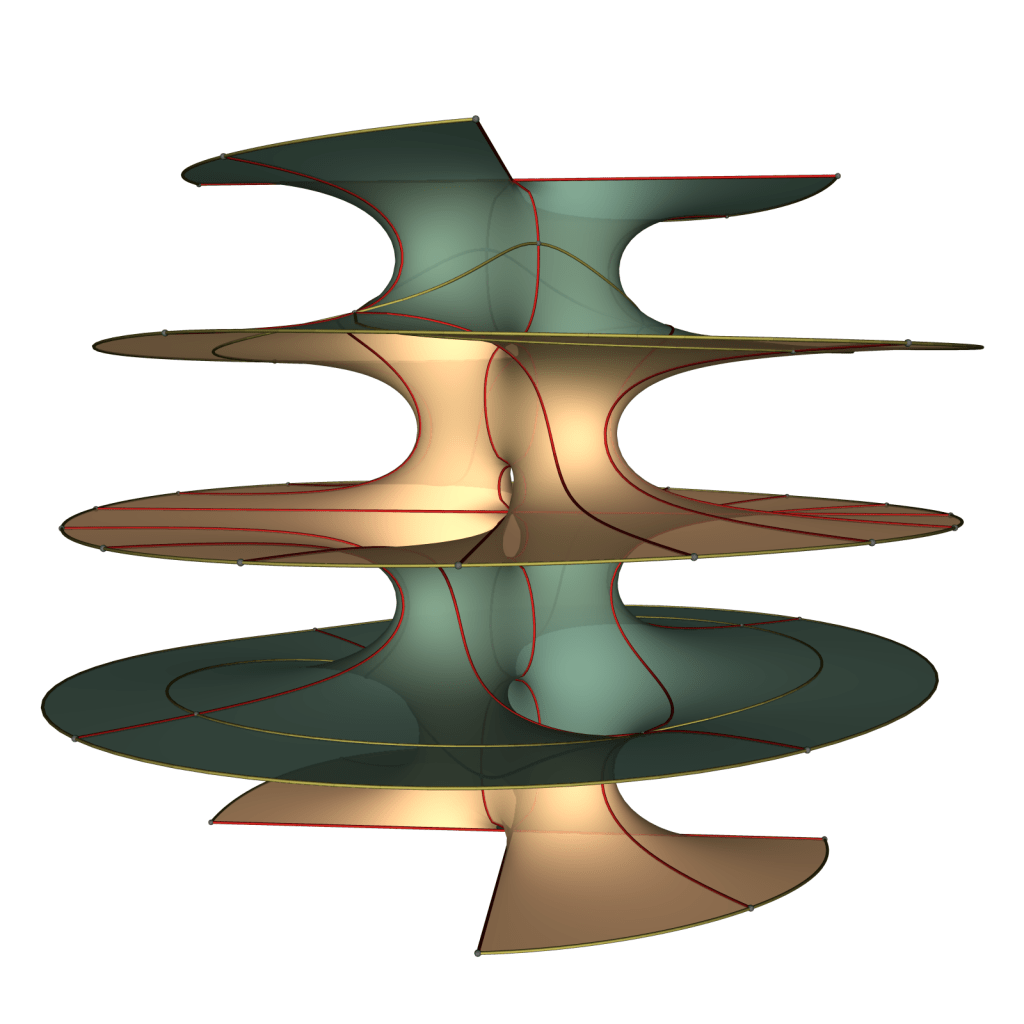

This is as far as I have pushed the numerical solution of the period problem. These surfaces exist for any values 1≤r≤s. I suspect that they can be deformed into screw motion invariant surfaces like CHM1,1. For what values of (r,s) these surfaces exist with higher dihedral symmetry is also uncertain. Ramazan Yol has numerically found that CHM1,2 exists with higher dihedral symmetry.
Resources
Mathematica Notebooks for (r,s) = (1,2), (1,3), (1,4), (1,5), (2,3)
PoVRay Sources for (r,s)- (1,2), (1,3), (1,4), (1,5), (2,3)
A paper about these surfaces